급수 (sin n) / n의 수렴성 증명

$\sum_{n=1}^{\infty}\frac{\sin n}{n}=\frac{\pi-1}{2}$

여기서는 위의 급수가 수렴함을 증명하겠습니다.

우선 디리클레 판정법(Dirichlet's test)을 증명합니다.

디리클레 판정법(Dirichlet's test)

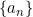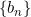$\inline \left \{ a_n \right \}$ 과 $\inline \left \{ b_n \right \}$ 이 다음을 만족하는 실수 수열이라고 하자.
1. 수열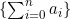 $\inline \left \{ \sum_{i=0}^{n}a_i \right \}$ 는 유계이다.
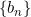2. $\inline \left \{ b_n \right \}$ 은 감소 수열이다.
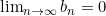
3. $\inline \lim_{n\to \infty}b_{n}=0$
그러면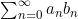 $\inline \sum_{n=0}^{\infty}a_n b_n$ 은 수렴한다.

- 증명 -
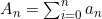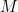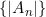$\inline A_{n}=\sum_{i=0}^{n}a_{n}$ 으로 두고 $\inline M$ 을 $\inline \left \{ \left | A_{n} \right | \right \}$ 의 상계라 하자.

그러면 아벨의 보조 정리에 의해,
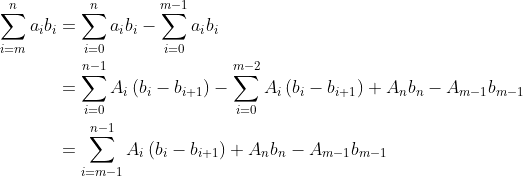
$\begin{align*} \sum_{i=m}^{n}a_{i}b_{i} &= \sum_{i=0}^{n}a_{i}b_{i}-\sum_{i=0}^{m-1}a_{i}b_{i}\\ &= \sum_{i=0}^{n-1}A_{i}\left ( b_{i}-b_{i+1} \right ) -\sum_{i=0}^{m-2}A_{i}\left ( b_{i}-b_{i+1} \right ) +A_{n}b_{n}-A_{m-1}b_{m-1} \\ &= \sum_{i=m-1}^{n-1}A_{i}\left ( b_{i}-b_{i+1} \right ) +A_{n}b_{n} - A_{m-1}b_{m-1} \end{align*}$

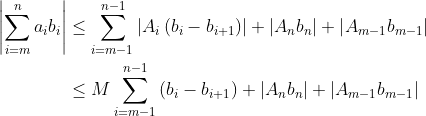
$\begin{align*} \left | \sum_{i=m}^{n}a_{i}b_{i} \right | &\leq \sum_{i=m-1}^{n-1} \left | A_{i}\left ( b_{i}-b_{i+1} \right ) \right | + \left |A_{n}b_{n} \right | + \left |A_{m-1}b_{m-1} \right | \\ &\leq M \sum_{i=m-1}^{n-1} \left ( b_{i}-b_{i+1} \right ) + \left |A_{n}b_{n} \right | + \left |A_{m-1}b_{m-1} \right | \end{align*}$

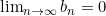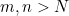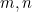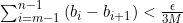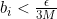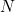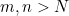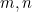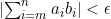$\inline \lim_{n\to \infty}b_{n}=0$ 이기 때문에 $\inline m, n > N$ 인 $\inline m, n$ 에 대해 $\inline \sum_{i=m-1}^{n-1} \left (b_{i} - b_{i+1} \right ) < \frac{\epsilon }{3M}$ 이고 $\inline b_{i} < \frac{\epsilon }{3M}$ 인 $\inline \epsilon$ 의 함수 $\inline N$ 이 존재한다. 그러면 $\inline m, n > N$ 인 $\inline m, n$ 에 대해 $\inline \left | \sum_{i=m}^{n}a_{i}b_{i} \right | < \epsilon$ 이 성립하고, 따라서 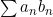$\inline \sum a_{n}b_{n}$ 은 수렴한다.

아벨의 보조 정리는 다음과 같습니다.

아벨의 보조 정리(Abel's lemma)

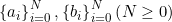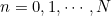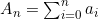$\inline \left \{ a_{i} \right \}_{i=0}^{N}, \left \{ b_{i} \right \}_{i=0}^{N} \left (N \geq 0 \right)$ 은 실수의 수열이다. $\inline n = 0, 1, \cdots, N$ 에 대해 $\inline A_{n} = \sum_{i=0}^{n}a_{i}$ 으로 두자. 그러면 다음 식이 성립한다.
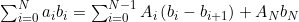
$\inline \sum_{i=0}^{N}a_{i}b_{i} = \sum_{i=0}^{N-1}A_{i} \left ( b_{i} - b_{i+1} \right ) +A_{N}b_{N}$

단,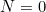 $\inline N=0$ 일 때 우변의 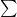$\inline \sum$ 는 0으로 생각한다. 곧, 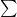$\inline \sum$ 에서 상계가 하계보다 작으면 그 값은 0이다.

- 증명 -
수학적 귀납법을 사용한다.
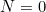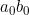$\inline N=0$ 일 때, 양변은 $\inline a_{0}b_{0}$ 로 같다.
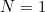$\inline N=1$ 일 때, 양변은 $\inline a_{0}b_{0}+a_{1}b_{1}$ 로 같다.
$\inline N \geq 2$ 일 때,
$\begin{align*} \sum_{i=0}^{N}a_{i}b_{i} &= \sum_{i=0}^{N-1}a_{i}b_{i}+a_{N}b_{N}\\ &= \sum_{i=0}^{N-2}A_{i}\left (b_{i} - b_{i+1} \right )+A_{N-1}b_{N-1}+a_{N}b_{N}\\ &= \sum_{i=0}^{N-1}A_{i}\left (b_{i} - b_{i+1} \right )-A_{N-1}\left(b_{N-1}-b_{N} \right )+A_{N-1}b_{N-1}+a_{N}b_{N}\\ &= \sum_{i=0}^{N-1}A_{i}\left (b_{i} - b_{i+1} \right )+A_{N}b_{N} \end{align*}$

이제 $\inline a_{n}=\sin n, b_{n} = \frac{1}{n}$ 으로 둡니다.

$\begin{align*} \sum_{k=0}^{n} a_{k} &= \sum_{k=0}^{n} \sin k\\ &= \Im\left \{ \sum_{k=0}^{n} e^{ik} \right \} \\ &= \Im\left \{ \sum_{k=0}^{n} \left (e^{i} \right )^{k} \right \}\\ &= \Im\left \{ \frac{1-\left( e^{i}\right )^{n+1}}{1-e^{i}} \right \} \end{align*}$

(여기에서 $\inline \Im \left \{ z \right \}$ 는 $\inline Im \left ( z \right )$ 와 같습니다. 위키피디아 Imaginary part 참고)
$\inline \left (e^{i} \right )^{n+1}$ 은 $\inline n$ 이 변함에 따라 복소평면에서 중심이 원점이고 반지름이 1인 원 위의 어떤 점에 대응됩니다.(극형식 참고) 따라서 위의 식은 유계임을 알 수 있습니다.
$\inline \frac{1}{n}$ 은 $\inline n$ 이 커짐에 따라 감소하고, $\inline \lim_{n\to \infty}\frac{1}{n}=0$ 입니다.

따라서 이 수열에 디리클레 판정법을 사용하면 $\inline \sum_{n=1}^{\infty}\frac{\sin n}{n}$ 는 수렴합니다.

참고로, 디리클레 적분(Dirichlet integral)이란 것이 있는데, 그 가운데 하나는 다음과 같습니다.
$\int_{0}^{\infty}\frac{\sin \omega }{\omega}d\omega=\frac{\pi}{2}$
다음은 디리클레 적분에 관한 위키피디아 웹 페이지입니다.
하이퍼링크(http://en.wikipedia.org/wiki/Dirichlet_integral)

'수학, 과학 > 수학' 카테고리의 다른 글

디리클레 판정법과 그 증명 (1)	2009.05.12

달빛이 비치는 곳

급수 (sin n) / n의 수렴성 증명

'수학, 과학 > 수학' 카테고리의 다른 글

티스토리툴바

급수 (sin n) / n의 수렴성 증명

'수학, 과학 > 수학' 카테고리의 다른 글

'수학, 과학/수학' Related Articles

티스토리툴바