디리클레 판정법과 그 증명

디리클레 판정법이란?

디리클레 판정법(Dirichlet's Test)은 급수의 수렴성을 검사하기 위한 방법 가운데 하나입니다. 수학자인 르죈 디리클레(Lejeune Dirichlet)의 이름을 땄습니다.

디리클레 판정법의 내용은 다음과 같습니다.

$\inline \left \{ a_n \right \}$ 과 $\inline \left \{ b_n \right \}$ 이 다음을 만족하는 실수 수열이라고 하자.
1. 수열 $\inline \left \{ \sum_{i=1}^{n}a_i \right \}$ 는 유계이다.
2. $\inline \left \{ b_n \right \}$ 은 감소 수열이다.
3. $\inline \lim_{n\to \infty}b_{n}=0$
그러면 $\inline \sum_{n=1}^{\infty}a_n b_n$ 은 수렴한다.

디리클레 판정법 증명

$\inline A_{n}=\sum_{i=1}^{n}a_{n}$ 으로 두고 $\inline M$ 을 $\inline \left \{ \left | A_{n} \right | \right \}$ 의 상계라 하자.

그러면 아벨의 보조 정리에 의해 다음이 성립한다.
$\begin{align*} \sum_{i=m}^{n}a_{i}b_{i} &= \sum_{i=1}^{n}a_{i}b_{i}-\sum_{i=1}^{m-1}a_{i}b_{i}\\ &= \sum_{i=1}^{n-1}A_{i}\left ( b_{i}-b_{i+1} \right ) -\sum_{i=1}^{m-2}A_{i}\left ( b_{i}-b_{i+1} \right ) +A_{n}b_{n}-A_{m-1}b_{m-1} \\ &= \sum_{i=m-1}^{n-1}A_{i}\left ( b_{i}-b_{i+1} \right ) +A_{n}b_{n} - A_{m-1}b_{m-1} \end{align*}$

$\begin{align*} \left | \sum_{i=m}^{n}a_{i}b_{i} \right | &\leq \sum_{i=m-1}^{n-1} \left | A_{i}\left ( b_{i}-b_{i+1} \right ) \right | + \left |A_{n}b_{n} \right | + \left |A_{m-1}b_{m-1} \right | \\ &\leq M \sum_{i=m-1}^{n-1} \left ( b_{i}-b_{i+1} \right ) + \left |A_{n}b_{n} \right | + \left |A_{m-1}b_{m-1} \right | \end{align*}$

$\inline \lim_{n\to \infty}b_{n}=0$ 이기 때문에 $\inline m, n > N$ 인 $\inline m, n$ 에 대해 $\inline \sum_{i=m-1}^{n-1} \left (b_{i} - b_{i+1} \right ) < \frac{\epsilon }{3M}$ 이고 $\inline b_{i} < \frac{\epsilon }{3M}$ 인 $\inline \epsilon$ 의 함수 $\inline N$ 이 존재한다. 그러면 $\inline m, n > N$ 인 $\inline m, n$ 에 대해 $\inline \left | \sum_{i=m}^{n}a_{i}b_{i} \right | < \epsilon$ 이 성립하고, 따라서 $\inline \sum a_{n}b_{n}$ 은 수렴한다.

교대 급수 판정법

디리클레 판정법의 따름 정리로 교대 급수 판정법(Alternating Series Test)이 있습니다. 교대 급수 판정법은 다른 방법으로도 증명할 수 있지만, 디리클레 판정법을 이용하면 곧바로 얻을 수 있습니다.
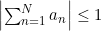디리클레 판정법에서 $a_{n} = \left ( -1 \right )^{n}$ 으로 두면 $\inline \left | \sum_{n=1}^{N} a_{n} \right | \leq 1$ 입니다. 이렇게 해서 얻게 되는 결과는 교대 급수 판정법과 같습니다. 곧, 다음 조건을 만족하면 $\inline \sum_{n=1}^{\infty} \left ( -1 \right )^{n} b_{n}$ 은 수렴합니다.
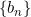(1) $\inline \left \{ b_n \right \}$ 은 감소 수열이다.
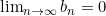
(2) $\inline \lim_{n\to \infty}b_{n}=0$

참고 자료

위키피디아(http://en.wikipedia.org/wiki/Dirichlet's_test)

플래닛 매스(http://planetmath.org/encyclopedia/DirichletsConvergenceTest.html)

'수학, 과학 > 수학' 카테고리의 다른 글

디리클레 판정법과 그 증명 (1)	2009.05.12
급수 (sin n) / n의 수렴성 증명 (1)	2009.05.02